RESEÑA HISTÓRICA
La historia de la trigonometría comienza con los babilonios y los egipcios. Estos últimos establecieron la medida de los ángulos en grados, minutos y segundos. Sin embargo, en los tiempos de la Grecia clásica, en el siglo II a.C. el astrónomo Hiparco de Nicea construyó una tabla de cuerdas para resolver triángulos. Comenzó con un ángulo de 71° y yendo hasta 180° con incrementos de 71°, la tabla daba la longitud de la cuerda delimitada por los lados del ángulo central dado que corta a una circunferencia de radio r. No se sabe el valor que Hiparco utilizó para r.
Tres siglos después, el astrónomo Claudio Ptolomeo utilizó r = 60, pues los griegos adoptaron el sistema numérico base 60 de los babilonios.
Durante muchos siglos, la trigonometría de Ptolomeo fue la introducción básica para los astrónomos. Su libro de Astronomía, el Almagesto, también tenía una tabla de cuerdas junto con la explicación de su método para compilarla, y a lo largo del libro mostraba ejemplos de cómo utilizar dicha tabla para calcular los elementos desconocidos de un triángulo a partir de los conocidos. El Teorema de Menelao utilizado para resolver triángulos esféricos fue autoría de Ptolomeo.
Al mismo tiempo, los astrónomos de la India habían desarrollado también un sistema trigonométrico basado en la función seno en vez de cuerdas como los griegos. Esta función seno, era la longitud del lado opuesto a un ángulo en un triángulo rectángulo de hipotenusa dada. Los matemáticos hindúes utilizaron diversos valores para ésta en sus tablas.
A finales del siglo VIII los astrónomos árabes trabajaron con la función seno y a finales del siglo X ya habían completado la función seno y las otras cinco funciones. También descubrieron y demostraron teoremas fundamentales de la trigonometría, tanto para triángulos planos como esféricos. Los matemáticos sugirieron el uso del valor r = 1 en vez de r = 60, y esto dio lugar a los valores modernos de las funciones trigonométricas
El Occidente latino se familiarizó con la trigonometría árabe a través de traducciones de libros de astronomía arábigos, que comenzaron a aparecer en el siglo XII. El primer trabajo importante en esta materia en Europa fue escrito por el matemático y astrónomo alemán Johann Müller Königsberg, llamado Regiomontano.
A principios del siglo XVII, el matemático escocés John Napier descubrió los logaritmos y, gracias a esto, los cálculos trigonométricos recibieron un gran empuje.
A mediados del siglo XVII, los científicos Isaac Newton y Gottfried Wilhelm Leibniz desarrollaron el Cálculo diferencial e integral. Uno de los fundamentos del trabajo de Newton fue la representación de muchas funciones matemáticas utilizando series infinitas de potencias de la variable x. Newton encontró la serie para sen x y series similares para cos x y tg x. Con la invención del Cálculo las funciones trigonométricas fueron incorporadas al Análisis, donde todavía hoy desempeñan un importante papel tanto en las matemáticas puras como en las aplicadas.
Por último, en el siglo XVIII, el matemático suizo Leonhard Euler demostró que las propiedades de la trigonometría eran producto de la aritmética de los números complejos y, además, definió las funciones trigonométricas utilizando expresiones con exponenciales de números complejos.
Etimología
La palabra "seno" deriva del término en latín, sinus, de una mala traducción (vía el árabe de la palabra en sánscrito, jiva o jya. Aryabhata utilizó el término ardha-jiva ("media-cuerda"), que fue acortado a jiva y, luego, transliterado por los árabes como jiba (جب). Traductores europeos como Roberto de Chester y Gerardo de Cremona en el siglo XII toledano confundieron jiba por jaib (جب), probablemente debido a que jiba (جب) y jaib (جب) se escriben igual en la escritura árabe (este sistema de escritura utiliza acentos en lugar de vocales y, en algunos formatos, los acentos no son escritos para facilitar la escritura, por lo que si los lectores no están familiarizados con el idioma pueden confundir palabras con las mismas letras, pero con diferente fonética). Las palabras "minuto" y "segundo" provienen de las frases latinas partes minutae primae y partes minutae secundae, que pueden ser burdamente traducidas como "primeras pequeñas partes" y "segundas pequeñas partes".
LECTURA Y BÚSQUEDA DE INFORMACIÓN HISTORIAL DE LA EVOLUCIÓN DE LA TRIGONOMÉTRICA
La historia de la trigonometría y de las funciones trigonométricas podría extenderse por más de 4000 años. Los babilonios determinaron aproximaciones de medidas de ángulos o de longitudes de los lados de los triángulos rectángulos. Varias tablas grabadas sobre arcilla seca lo testimonian. Así, por ejemplo, una tablilla babilónica escrita en cuneiforme, denominada Plimpton 322 (en torno al 1900 a. C.) muestra quince ternas pitagóricas y una columna de números que puede ser interpretada como una tabla de funciones trigonométricas;1 sin embargo, existen varios debates sobre si, en realidad, se trata de una tabla trigonométrica.
ÁNGULOS Y SUS MEDIDAS
Ángulos
Clases de ángulos según su suma
Ángulos entre paralelas y una recta transversal
SISTEMA DE MEDICIÓN ANGULAR
En la medida de ángulos, y por tanto en trigonometría, se emplean cuatro unidades, si bien la más utilizada en la vida cotidiana es el Grado sexagesimal, en matemáticas es el Radián la más utilizada, y se define como la unidad natural para medir ángulos, el Grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografía, arquitectura o en construcción.
- Radián: unidad angular natural en trigonometría, será la que aquí utilicemos. En una circunferencia completa hay 2π radianes.
- Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.
- Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.
- Horario: su unidad de medida es el ángulo de 1 hora, que equivale a la sexta parte del ángulo recto.
Relación entre los Sistemas de medición de ángulos:
180º -------- π rad. ----------- 200G----------- 12 hs
Radián
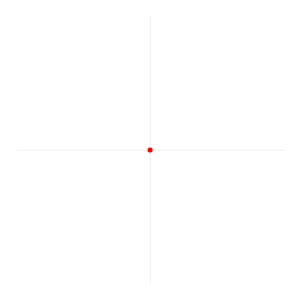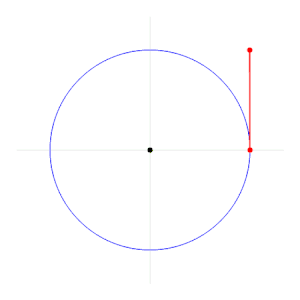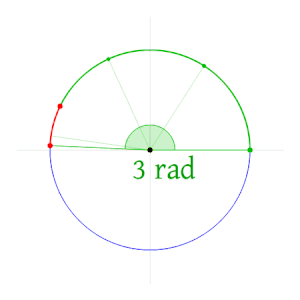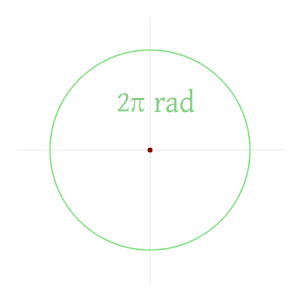
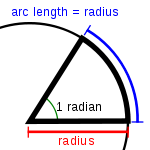
El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia y abarca un arco cuya longitud es igual a la del radio. Su símbolo es rad. Hasta 1995 tuvo la categoría de unidad suplementaria en el Sistema Internacional de Unidades, junto con el estereorradián. A partir de ese año, y hasta el momento presente, ambas unidades figuran en la categoría de unidades derivadas.
Esta unidad se utiliza primordial-mente en física, cálculo infinitesimal, trigonometría, geometría, etc.
Definición
El ángulo formado por dos radios de una circunferencia, medido en radianes, es igual a la longitud del arco que delimitan los radios dividida entre el radio; es decir, θ = s/r, donde θ es ángulo, s es la longitud de arco, y r es el radio. Por tanto, el ángulo completo,  , que subtiende una circunferencia de radio r, medido en radianes, es:
, que subtiende una circunferencia de radio r, medido en radianes, es:
 , que subtiende una circunferencia de radio r, medido en radianes, es:
, que subtiende una circunferencia de radio r, medido en radianes, es:Utilidad
El radián es una unidad sumamente útil para medir ángulos, puesto que simplifica los cálculos, ya que los más comunes se expresan mediante sencillos múltiplos o divisores de π.
Análisis dimensional
El radián es la unidad natural en la medida de los ángulos. Por ejemplo, la función seno de un ángulo x expresado en radianes cumple:
donde x se expresa en radianes.
Equivalencias
- La equivalencia entre grados sexagesimales y radianes es: π rad = 180°. Por tanto
1 radián = 57.29577951... grados sexagesimales y
1 grado sexagesimal = 0.01745329252... radianes.
- La equivalencia entre grados centesimales y radianes es: π rad = 200g
La tabla muestra la conversión de los ángulos más comunes.
| Grados | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| Radianes | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 7π/6 | 5π/4 | 4π/3 | 3π/2 | 5π/3 | 7π/4 | 11π/6 | 2π |
Otras unidades de medida de ángulos convencionales son el grado sexagesimal, el grado centesimal y, en astronomía, la hora.
- El Radián tiene una unidad derivada llamada radián por segundo (rad/s) (velocidad angular). Esta tiene una equivalencia con las rpm. Las equivalencias se pueden calcular fácilmente con la ecuación que sigue:
- De rpm a π rad/s
 que con la ecuación simplificada:
que con la ecuación simplificada:
- De π rad/s a rpm
 que con la ecuación simplificada:
que con la ecuación simplificada:
Conversiones entre grados y radianes
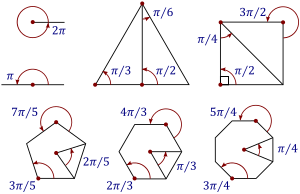
Los grados y los radianes son dos diferentes sistemas para medir ángulos. Un ángulo de 360° equivale a 2π radianes; un ángulo de 180° equivale a π radianes (recordemos que el número π ≈ 3,14159265359…).
Las equivalencias de los principales ángulos se muestran en las siguientes figuras:
Para convertir grados en radianes o viceversa, partimos de que 180° equivalen a π radianes; luego planteamos una regla de tres y resolvemos.
-
- Ejemplo A
Convertir 38° a radianes:
Primero planteamos la regla de tres. Nótese que la x va arriba, en la posición de los radianes.
Despejamos x, también simplificamos.
Por último obtenemos el equivalente decimal:
x = 0,6632 radianes.
-
- Ejemplo B
Convertir 2,4 radianes a grados.
Primero planteamos la regla de tres. Nótese que la x va abajo, en la posición de los grados.
Despejamos x.
Por último obtenemos el equivalente decimal:
x = 137.5099°".
Grado sexagesimal
Un grado sexagesimal es el ángulo central subtendido por un arco cuya longitud es igual a 1/360 de la circunferencia. Es la nonagésima (1/90) parte de un ángulo recto.
El grado sexagesimal, como unidad del sistema de medida de ángulos sexagesimal, está definido partiendo de que un ángulo recto tiene 90° (90 grados sexagesimales), y sus divisores: el minuto sexagesimal y el segundo sexagesimal, están definidos del siguiente modo:
- 1 ángulo recto = 90° (grados sexagesimales).
- 1 grado sexagesimal = 60′ (minutos sexagesimales).
- 1 minuto sexagesimal = 60″ (segundos sexagesimales).
Notación sexagesimal
Podemos expresar una cantidad en grados, minutos y segundos, las partes de grado inferiores al segundo se expresan como parte decimal de segundo, ejemplo:
- 12°34′34″
- 13°3′23,8″
- 124°45′34,70″
- -2°34′10″
Teniendo cuidado como norma de notación, no dejar espacio entre las cifras, es decir:
escribir 12°34′34″ y no 12° 34′ 34″
Podemos también representar en forma decimal la medida de un ángulo en representación sexagesimal teniendo en cuenta que:
1’ = (1/60)° = 0,01666667° (redondeando a ocho dígitos)
1” = (1/60)′ = (1/3600)° = 0,00027778°
Así 12°15′23″ = 12° + 15(1/60)° + 23(1/3600)° ≈ 12,25639°
Notación decima
Una cantidad en grados se puede expresar en forma decimal, separando la parte entera de la fraccionaria con la coma decimal, se divide en 60 en la forma normal de expresar cantidades decimales, lo que se busca es transformar en minuto y el segundo números decimales, por ejemplo.
- 23,2345°
- 12,32°
- -50,265°
- 123,696°
Relación entre radianes y grados sexagesimales
Se parte de la base de que una circunferencia completa tiene  radianes, y que una circunferencia tiene 360° sexagesimales, luego tenemos:
radianes, y que una circunferencia tiene 360° sexagesimales, luego tenemos:
 radianes, y que una circunferencia tiene 360° sexagesimales, luego tenemos:
radianes, y que una circunferencia tiene 360° sexagesimales, luego tenemos:
Haciendo una regla de tres simple se llega a que el factor de conversión de grados sexagesimales a radianes es:
Luego tenemos que, para un ángulo x dado en grados, su equivalente X en radianes es:
y viceversa (si tenemos que, para un ángulo X dado en radianes, su equivalente x en grados es):

- 1 grado centesimal = 100 minutos centesimales (100m o 100c)
- 1 minuto centesimal = 100 segundos centesimales (100s o 100cc)
Grado centesimal
El grado centesimal o gon —también llamado gradián (plural: gradianes), pero no gonio1 — es una unidad de medida de ángulos planos, alternativa al grado sexagesimal y, como este, no perteneciente al Sistema Internacional de Unidades, cuyo valor se define como el ángulo central subtendido por un arco cuya longitud es igual a 1/400 de la circunferencia. La circunferencia se divide, por tanto, en 400 gon y un ángulo recto en cien gon, lo que permite determinar que un grado centesimal equivale a nueve décimas partes del grado sexagesimal. Su símbolo es una "g" minúscula en superíndice colocada tras la cifra (por ejemplo, 12,4574g).
La denominación de gon suele restringirse a los ámbitos especializados de la topografía y la ingeniería civil, donde es muy utilizada esta unidad de medida para definir el valor de los ángulos. La denominación de gradián se emplea en las calculadoras, en las que suele representarse con la abreviatura grad.
Sus divisores son:
Existía una denominación anterior de esta unidad como grado centígrado. Para evitar confusiones, en 1948 la unidad homónima de temperatura del mismo nombre pasó a denominarse oficialmente grado Celsius, aunque popularmente el grado celsius se siga denominando centígrado.3 Esto es parcialmente incorrecto, ya que la escala Kelvin también es centígrada (es una escala que toma de referencia 100 partes iguales, en este caso, punto de congelación y ebullición del agua destilada) y el término sería ambiguo.
Relación con el tamaño de la Tierra
Atendiendo a la definición de metro utilizada en 1889, un kilómetro debería corresponder a la longitud de un arco de meridiano cuya amplitud es un minuto centesimal; aunque mediciones posteriores más precisas del tamaño de la Tierra mostraron que existen diferencias.
Equivalencias
El grado centesimal surge de la división del plano cartesiano en cuatrocientos ángulos iguales, con vértice común. Cada cuadrante posee una amplitud 100 grados centesimales, y la suma de los cuatro cuadrantes mide 400 grados centesimales.
- Equivalencia entre grados sexagesimales y centesimales
- 0° = 0g
- 90° = 100g
- 180° = 200g
- 270° = 300g
- 360° = 400g
- Ejemplo
Los siguientes valores angulares son equivalentes:
- 23° 47' 35" grados sexagesimales
- 23,7931º grados sexagesimales con fracción decimal
- 26g 43c 67cc gons con minutos y segundos centesimales
- 26,4367g gons o grados centesimales
Los minutos y segundos de gon se corresponden con la fracción decimal de gon, cosa que no ocurre con los grados sexagesimales. No deben confundirse los grados centesimales con el uso de fracciones decimales para expresar ángulos en grados sexagesimales.
Conversión de ángulos comunes
| Unidades | Valores | |||||||
|---|---|---|---|---|---|---|---|---|
| Revolución | 0 |  |  |  |  |  |  |  |
| Grados sexagesimales | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radianes | 0 |  |  |  |  |  | 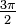 |  |
| Grados centesimales | 0g |  | 50g |  | 100g | 200g | 300g | 400g |
CONVERSIÓN DE SISTEMAS DE MEDICIÓN ANGULAR
.gif)
CIRCULO TRIGONOMÉTRICO
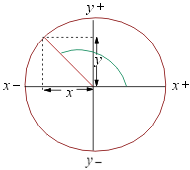
También conocido como goniométrico, es aquel círculo cuyo centro coincide con el origen de coordenadas del plano cartesiano y cuyo radio mide la unidad. El círculo trigonométrico tiene la ventaja de ser una herramienta práctica en el manejo de los conceptos de trigonometría, pero al mismo tiempo es un apoyo teórico, pues ayuda a fundamentar y tener una idea precisa y formal de las funciones trigonométricas. Atreves del círculo trigonométrico se puede obtener de forma manual o analítica el valor aproximado de las razones trigonométricas para un ángulo determinado si se dispone de los instrumentos geométricos necesarios.
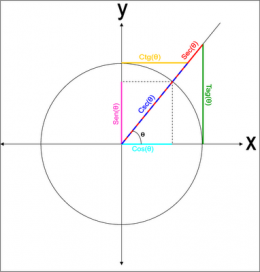
Características
Se toma como base un círculo de radio r = 1 con centro o, en el origen en el plano cartesiano. Se considera un ángulo arbitrario medido a partir del eje x positivo y en sentido positivo; o sea, en sentido contrario a las manecillas del reloj; todo ángulo puede ser colocado (y de una sola manera) de forma tal que su vértice coincida con el origen de coordenada , uno de sus lados (llamado lado inicial) coincide con la semirrecta OA y el otro lado (llamado lado terminal) quede ubicado ( a partir del inicial) en la zona de barrida en sentido contrario a la manecilla del reloj
Si la semirrecta r =1 la hacemos rotar en sentido contrario a la manecilla del reloj, describe un círculo dividido en 4 cuadrantes (I, II, III, IV). Antes de que la semirrecta OP comience a rotar, coincide con el rayo OA, formando un ángulo de 0°. Cuando la semirrecta OP rota, describe un ángulo α, el cual alcanza su máximo (describiendo un círculo completo) a 360° (2π medido en radianes). De esta forma el lado terminal de cada ángulo interseca en un único punto a la [circunferencia] y podemos asociar al ángulo en ese punto de manera unívoca.
Razones trigonométricas
Si se rota la semirrecta OP de radio r rota hasta formar un ángulo α, si proyectamos el punto P hasta el eje X,Y, se obtienen dos segmentos; sobre el eje Y se proyecta el segmento OB denominado seno del ángulo α (Seno α), sobre el eje X se proyecta el segmento OA denominado coseno del ángulo α (cos α), formando un triángulo rectángulo OAP, cuyo lado AP se le denomina cateto opuesto al ángulo α, el lado OA es el cateto adyacente al ángulo α, mientras que el lado OP= r se denomina hipotenusa. Del triángulo rectángulo anterior podemos denotar las razones trigonométricas siguientes:
- sen α = PA/r
- cos α = OA/r
- tang α = PA/OA
- cot α= OA/PA
Seno del ángulo α
A partir del ángulo α y la semirrecta r se obtiene el punto P, al trazar una perpendicular desde dicho punto y hacia el eje Y se obtiene un segmento OB = AP que se denomina seno del ángulo α (se denota como sen α), también se determina a través de la razón (PA/r).
Coseno del ángulo α
A partir del ángulo α y la semirrecta r se obtiene el punto P, al trazar una perpendicular desde dicho punto y hasta el eje X se obtiene un segmento OA = BP que se denomina coseno del ángulo α (se denota como cos α), también se determina a través de la razón OA/r.
Tangente del ángulo α
Si trazamos una semirrecta EC tangente a la circunferencia por el punto E, que toque la semirrecta OD (prolongación de la semirrecta r), se forma el segmento EC que se denomina tangente del ángulo α (se denota como tang α); también se determina a través de la razón PA/OA.
Cotangente del ángulo α
Si trazamos una semirrecta FD, tangente al punto F y que toque la semirrecta OD, se forma un segmento FD denominado Cotangente del ángulo α (se denota como cot α); también se determina a través de la razón OA/PA.
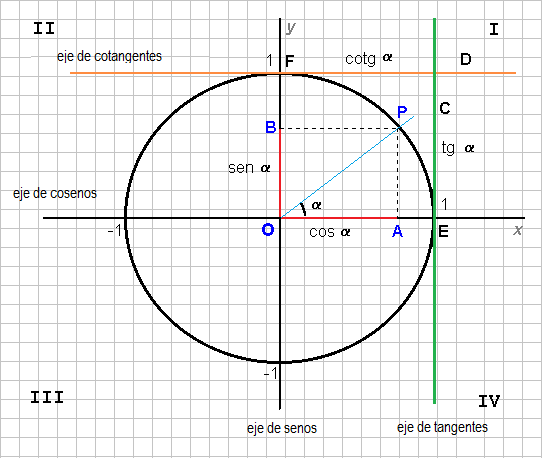
Cuadrantes del círculo trigonométrico
Si dividimos el círculo trigonométrico en 4 partes iguales se obtiene como resultado que cada [ángulo] consecutivo mide 90° (π/2 rd), cada una de las partes obtenidas se conoce como cuadrantes del círculo trigonométrico. En cada cuadrante los parámetros seno, coseno, tangente y cotangente cambian su valor numérico con el aumento o disminución del ángulo α, este hecho lo corrobora las razones trigonométricas anteriores.
Primer cuadrante
Segundo cuadrante
Parámetro Signo Seno + Coseno - Tangente - Cotangente -
En el segundo cuadrante (II), con el aumento del ángulo α, disminuyen el sen α y el cos α, por lo que lo hacen tambiéntang α y cot α, alcanzando su mínimo valor a 180° (π).
Tercer cuadrante
Parámetro Signo Seno - Coseno - Tangente + Cotangente +
En el tercer cuadrante (III), con el aumento del ángulo α, disminuyen el sen α y el cos α, la tang α aumenta su valor, mientras que la cot α disminuye dado que (a partir de que seno y el coseno son negativos y la relación existente entre ellos) hasta alcanzar su mínimo o máximo valor a 270° (3π/2).
Cuarto cuadrante
Parámetro Signo Seno - Coseno + Tangente - Cotangente -
En el cuarto cuadrante (IV), con el aumento del ángulo α, dirminuye el sen α, mientras que aumenta el cos α por lo que aumenta la cot α, mientras que disminuye la tang α y el, hasta alcanzar su máximo y mínimo valor a 360° (2π).
Parámetro Signo Seno + Coseno + Tangente + Cotangente +
En el primer cuadrante (I), con el aumento del [ángulo] α, disminuye el cos α y la cot α, mientras que aumenta la tang α y el sen α, hasta alcanzar su máximo o mínimo valor a 90° (π/2).
Ángulo en Posición Normal :Llamado también ángulo en posición canónica o estándar; es aquel ángulo trigonométrico cuyo vértice coincide con el origen del sistema cartesiano, su lado inicial coincide con el semieje positivo de abscisas y su lado se ubicará en cualquier región del plano, siendo el que indique a que cuadrante pertenece dicho ángulo. En el gráfico adjunto por ejemplo : a, b y q son ángulos en posición normal, cumpliéndose: a Î IC; b Î IIC; q Î IIIC.
 • Ángulos CuadrantalesSe va a denominar ángulo cuadrantal a aquel ángulo en posición normal cuyo lado final coincide con cualquiera de los semiejes cartesianos. Las medidas de estos ángulos es siempre múltiplo de 90º.
• Ángulos CuadrantalesSe va a denominar ángulo cuadrantal a aquel ángulo en posición normal cuyo lado final coincide con cualquiera de los semiejes cartesianos. Las medidas de estos ángulos es siempre múltiplo de 90º.Estos ángulos no pertenecen a cuadrante alguno
• Ángulos Coterminales
Son aquellos ángulos en posición normal que tienen el mismo lado final; y su diferencia de medidas es siempre múltiplo de 360º.

• Definición de las razones trigonométricas de un ángulo en Posición NormalPara definir o hallar las R.T. de un ángulo en posición normal; se debe conocer un punto perteneciente a su lado final.
En el gráfico; para "a"; tendremos:
 Por ejemplo:
Por ejemplo:
Se debe notar que ahora las R.T. pueden tener signo negativo; dependiendo del cuadrante en el que se ubique el ángulo considerado.
* Signos de las R.T.Dependiendo del cuadrante en el que se ubique un ángulo en posición normal; podemos establecer el siguiente criterio práctico para los signos:

* PropiedadLas Razones trigonométricas de los ángulos coterminales son respectivamente iguales.
* R.T. de los Ángulos CuadrantalesLas R.T. de los ángulos cuadrantales principales se calculan con las mismas definiciones aplicadas a cualquier ángulo en posición normal. El resultado se muestra en el siguiente cuadro:

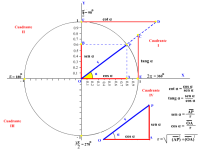
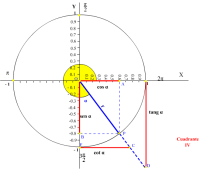
LINEAS TRIGONOMÉTRICAS
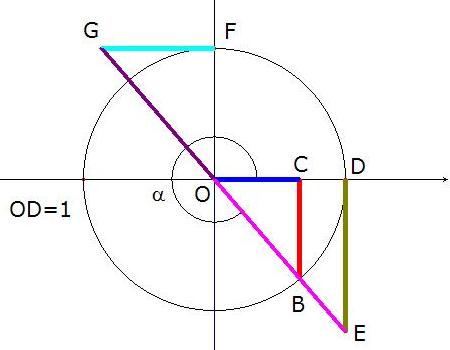
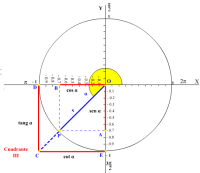
Si consideramos r=1 , entonces se obtiene la circunferencia goniométrica, que nos da inmediatamente el valor de las razones trigonométricas y su representación gráfica como se explica a continuación para un ángulo del primer cuadrante:
 |
sen α = BC OB = BC 1 =BC = y = ordenada cos α = OC OB = OC 1 =OC = x = abscisa
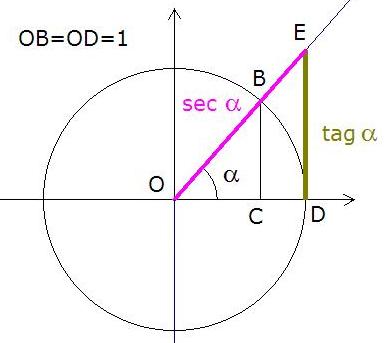 |
tg α = BC OC = DE OD =DE sec α = OB OC = OE OD = OE 1 =OE
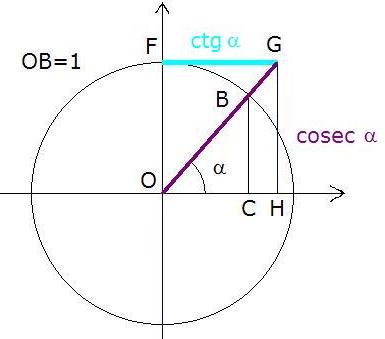 |
ctg α = OC BC = OH GH = FG OF = FG 1 =FG cosec α = OB BC = OG GH = OG OF = OG 1 =OG
En los demás cuadrantes, el estudio es análogo, teniendo en cuenta que para obtener la tangente, la cosecante, la secante y la cotangente se prolonga el lado extremo del ángulo hasta que corte a las rectas tangentes a la circunferencia en los puntos (1,0) y (0,1).
Segundo cuadrante
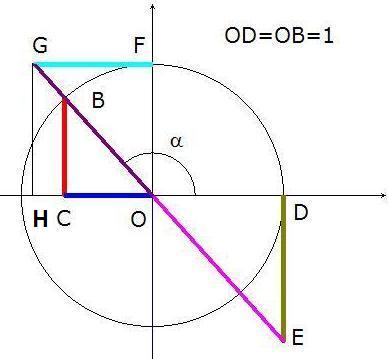
ctg α = OC BC = OH GH = FG OF = FG 1 =FG cosec α = OB BC = OG GH = OG OF = OG 1 =OG
Tercer cuadrante
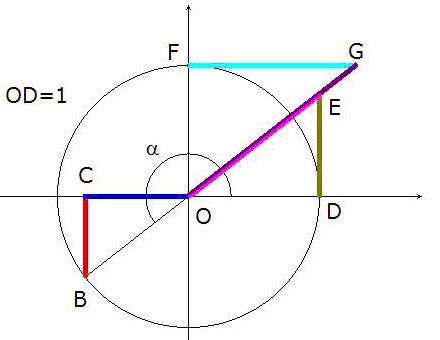
sen α = CB ; cos α = OC ; tg α = DE cosec α = OG ; sec α = OE ; ctg α = FG
Cuarto cuadrante
sen α = CB ; cos α = OC ; tg α = DE cosec α = OG ; sec α = OE ; ctg α = FG
SIGNOS DE LAS RAZONES TRIGONOMÉTRICAS
Los signos de las funciones trigonométricas varían dependiendo del cuadrante en el que se encuentren, aquí te mostraré que signo tiene cada una en cada cuadrante
sen α = c.opuesto/hipotenusa
cos α = c.adyacente/hipotenusa
tang α = c.opuesto/ c.adyacente
Primer cuadrante

En este cuadrante el cateto adyacente está sobre el eje “x” y el cateto opuesto sobre el eje “y”, la hipotenusa es el radio de la circunferencia.
Como el c, opuesto, c. adyacente y la hipotenusa son positivos, todas las funciones trigonométricas son positivas en el primer cuadrante.
Segundo cuadrante

En este cuadrante, el cateto adyacente es negativo y el cateto opuesto es positivo también es positiva la hipotenusa. Por lo que el coseno, la tangente, la secante y la cotangente son negativas.
Tercer cuadrante

En este cuadrante el cateto adyacente y el cateto opuesto son negativos y la hipotenusa es positiva. Por lo tanto la tangente y la cotangente resultan positivas y las demás negativas.
Cuarto cuadrante

En este cuadrante el cateto adyacente es positivo y el cateto opuesto es negativo y la hipotenusa es positiva. Por lo tanto solo el coseno y la secante serán positivas.
Con lo anterior, y aplicando las identidades trigonométricas fundamentales, considerando sólo su signo, obtenemos que:
I
|
II
|
III
|
IV
| |
seno
|
+
|
+
|
-
|
-
|
coseno
|
+
|
-
|
-
|
+
|
tangente
|
+
|
-
|
+
|
-
|
cotangente
|
+
|
-
|
+
|
-
|
secante
|
+
|
-
|
-
|
+
|
cosecante
|
+
|
+
|
-
|
-
|
FUNCIONES TRIGONOMÉTRICAS
Las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.
Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

Conceptos básicos
Las funciones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectánguloasociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.
Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente ; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).
| Función | Abreviatura | Equivalencias (en radianes) |
|---|---|---|
| Seno | sen, sin | 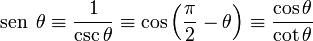 |
| Coseno | cos |  |
| Tangente | tan, tg |  |
| Cotangente | ctg (cot) |  |
| Secante | sec |  |
| Cosecante | csc (cosec) | 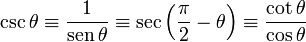 |
Definiciones respecto de un triángulo rectángulo
Para definir las razones trigonométricas del ángulo:  , del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:
, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:
 , del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:
, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:- La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
- El cateto opuesto (a) es el lado opuesto al ángulo
 .
. - El cateto adyacente (b) es el lado adyacente al ángulo
 .
.
Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes(o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:
1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:
El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo  , en cuyo caso se trata de triángulos semejantes.
, en cuyo caso se trata de triángulos semejantes.
 , en cuyo caso se trata de triángulos semejantes.
, en cuyo caso se trata de triángulos semejantes.
2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:
3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:
4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:
5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:
6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:
Funciones trigonométricas de ángulos notables
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| sen | 0 |  |  |  | 1 |
| cos | 1 |  |  |  | 0 |
| tan | 0 | 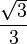 | 1 | 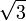 |  |
Definición para un número real cualquiera[editar]
No es posible utilizar la definición dada anteriormente, un coseno de  para valores de
para valores de  menores o iguales a 0 o valores mayores o iguales a π/2, pues no se podría construir un triángulo rectángulo tal que uno de sus ángulos mida
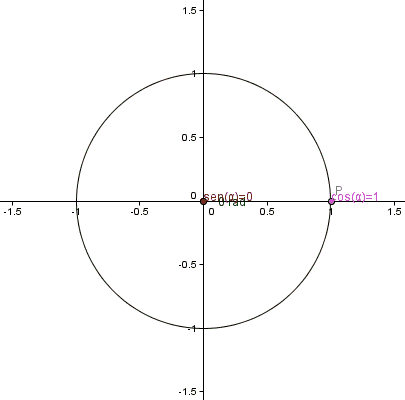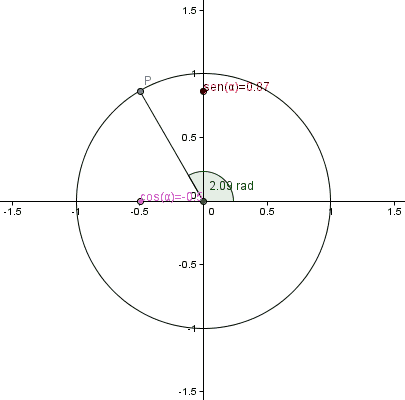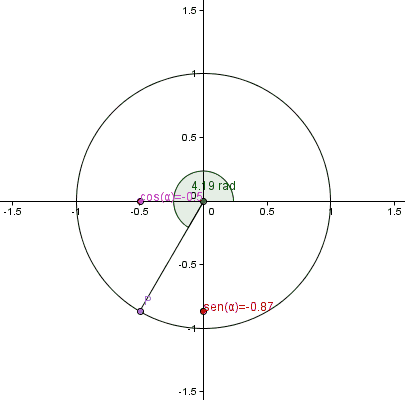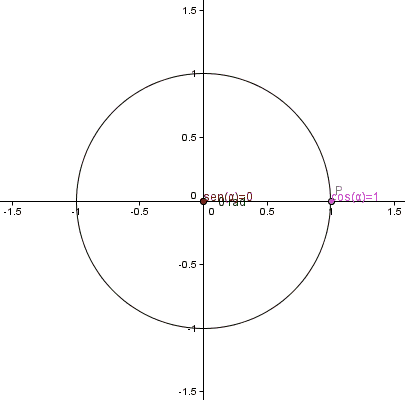
menores o iguales a 0 o valores mayores o iguales a π/2, pues no se podría construir un triángulo rectángulo tal que uno de sus ángulos mida  radianes. Para definir los valores de estas funciones para valores comprendidos entre 0 y 2π, se utilizará entonces una circunferencia unitaria, centrada en el origen de coordenadas del plano cartesiano. Se definirán las funciones trigonométricas seno y coseno como la abscisa y la ordenada, respectivamente, de un punto P perteneciente a la circunferencia, siendo
radianes. Para definir los valores de estas funciones para valores comprendidos entre 0 y 2π, se utilizará entonces una circunferencia unitaria, centrada en el origen de coordenadas del plano cartesiano. Se definirán las funciones trigonométricas seno y coseno como la abscisa y la ordenada, respectivamente, de un punto P perteneciente a la circunferencia, siendo  el ángulo, medido en radianes, entre el semieje positivo x y el segmento que une el origen con P.
el ángulo, medido en radianes, entre el semieje positivo x y el segmento que une el origen con P.
 para valores de
para valores de  menores o iguales a 0 o valores mayores o iguales a π/2, pues no se podría construir un triángulo rectángulo tal que uno de sus ángulos mida
menores o iguales a 0 o valores mayores o iguales a π/2, pues no se podría construir un triángulo rectángulo tal que uno de sus ángulos mida  radianes. Para definir los valores de estas funciones para valores comprendidos entre 0 y 2π, se utilizará entonces una circunferencia unitaria, centrada en el origen de coordenadas del plano cartesiano. Se definirán las funciones trigonométricas seno y coseno como la abscisa y la ordenada, respectivamente, de un punto P perteneciente a la circunferencia, siendo
radianes. Para definir los valores de estas funciones para valores comprendidos entre 0 y 2π, se utilizará entonces una circunferencia unitaria, centrada en el origen de coordenadas del plano cartesiano. Se definirán las funciones trigonométricas seno y coseno como la abscisa y la ordenada, respectivamente, de un punto P perteneciente a la circunferencia, siendo  el ángulo, medido en radianes, entre el semieje positivo x y el segmento que une el origen con P.
el ángulo, medido en radianes, entre el semieje positivo x y el segmento que une el origen con P.
Puede observarse que estas funciones toman valores entre -1 y 1. Nótese que para valores entre 0 y π/2, los valores obtenidos para el seno y el coseno con esta definición, coinciden con los obtenidos utilizando la noción de razón trigonométrica. Si el valor de x está fuera del intervalo [0,2π], puede descomponerse como x=2kπ+x' siendo k un número entero y x' un valor entre 0 y 2π. Se asignará a x los mismos valores de seno y coseno que los asignados a x', ya que puede interpretarse a x como un ángulo coterminal con x', y por lo tanto, las coordenadas del punto P serán las mismas en ambos casos.
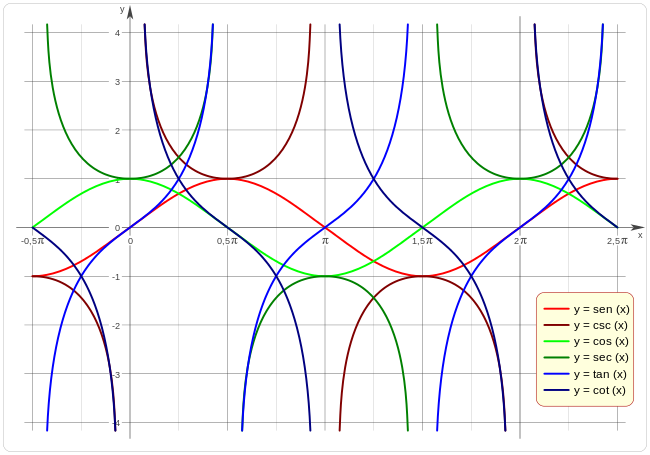
Representación gráfica
Funciones trigonométricas de ángulo doble
Sabiendo las funciones trigonométricas de la suma de dos ángulos, se pueden determinar las funciones trigonométricas de ángulo doble al plantear que 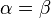
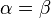
Para la fórmula del coseno del ángulo doble se pueden presentar otras dos formas alternativas con el uso de las identidades pitagóricas: Convirtiendo  a términos de
a términos de  , o convirtiendo
, o convirtiendo  a términos de
a términos de  :
:
 a términos de
a términos de  , o convirtiendo
, o convirtiendo  a términos de
a términos de  :
:
Para la tangente del ángulo doble se procede de la misma manera:
Para productos de dos funciones sinusoidales complementarias, se tiene que:
Y para el caso alternativo:
Definiciones analíticas
La definición analítica más frecuente dentro del análisis real se hace a partir de ecuaciones diferenciales. Usando la geometría y las propiedades de los límites, se puede demostrar que la derivada del seno es el coseno y la derivada del coseno es el seno con signo negativo. (Aquí, como se hace generalmente en cálculo, todos los ángulos son medidos en radianes).
El teorema de Picard-Lindelöf de existencia y unicidad de las ecuaciones diferenciales lleva a que existen las funciones anteriores que se llaman respectivamente seno y coseno, es decir:
Esta definición analítica de las funciones trigonométricas permite una definición no-geométrica del número π, a saber, dicho número es el mínimo número real positivo que es un cero de la función seno.
Series de potencias
A partir de la definición anterior pueden establecerse que las funciones seno y coseno son funciones analíticas cuya serie de Maclaurin viene dada por:
Estas identidades son a veces usadas como las definiciones de las funciones seno y coseno. Con frecuencia se utilizan como el punto de partida para el tratamiento riguroso de las funciones trigonométricas y sus aplicaciones (por ejemplo en las Series de Fourier), debido a que la teoría de las series infinitas puede ser desarrollada a partir de la base del sistema de números reales, independientemente de cualquier consideración geométrica. La diferenciabilidad y continuidad de estas funciones es entonces establecida a partir de las definiciones de series por sí misma.
Relación con la exponencial compleja
Existe una relación importante entre la exponenciación de números complejos y las funciones trigonométricas según la fórmula de Euler:
Esta relación puede probarse usando el desarrollo en serie de Taylor para la función exponencial y el obtenido en la sección anterior para las funciones seno y coseno. Separando ahora en parte real e imaginaria en la expresión anterior se encuentran las definiciones de seno y coseno en términos de exponenciales complejas:
A partir de ecuaciones diferenciales
Las funciones seno y coseno satisfacen la igualdad:
Es decir, la segunda derivada de cada función es la propia función con signo inverso. Dentro del espacio funcional de dos dimensiones V, que consiste en todas las soluciones de esta ecuación,
- la función seno es la única solución que satisface la condición inicial
 y
y - la función coseno es la única solución que satisface la condición inicial
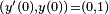 .
.
Dado que las funciones seno y coseno son lineal mente independientes, juntas pueden formar la base de V. Este método para definir las funciones seno y coseno es esencialmente equivalente a utilizar la fórmula de Euler. Además esta ecuación diferencial puede utilizarse no solo para definir al seno y al coseno, con ella también se pueden probar las identidades trigonométricas de las funciones seno y coseno.
Además, la observación de que el seno y el coseno satisfacen y′′ = −y implica que son funciones eigen del operador de la segunda derivada.
La función tangente es la única solución de la ecuación diferencial no lineal
satisfaciendo la condición inicial y(0) = 0. Existe una interesante prueba visual de que la función tangente satisface esta ecuación diferencial.
Funciones trigonométricas inversas
Las tres funciones trigonométricas inversas comúnmente usadas son:
- Arcoseno es la función inversa del seno de un ángulo. El significado geométrico es: el arco cuyo seno es dicho valor.
La función arcoseno real es una función ![\left[-1,1\right] \to \left[0,2\pi \right]\,](https://upload.wikimedia.org/math/7/f/3/7f39657b46007d21e643b0dbd51325e6.png) , es decir, no está definida para cualquier número real. Esta función puede expresarse mediante la siguienteserie de Taylor:
, es decir, no está definida para cualquier número real. Esta función puede expresarse mediante la siguienteserie de Taylor:
![\left[-1,1\right] \to \left[0,2\pi \right]\,](https://upload.wikimedia.org/math/7/f/3/7f39657b46007d21e643b0dbd51325e6.png) , es decir, no está definida para cualquier número real. Esta función puede expresarse mediante la siguienteserie de Taylor:
, es decir, no está definida para cualquier número real. Esta función puede expresarse mediante la siguienteserie de Taylor:- Arcocoseno es la función inversa del coseno de un ángulo. El significado geométrico es: el arco cuyo coseno es dicho valor.
Es una función similar a la anterior, de hecho puede definirse como:
- Arcotangente es la función inversa de la tangente de un ángulo. El significado geométrico es: el arco cuya tangente es dicho valor.
A diferencia de las anteriores la función arcotangente está definida para todos los reales. Su expresión en forma de serie es:
Representación gráfica
IDENTIDADES TRIGONOMÉTRICAS
Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y las operaciones aritméticas involucradas).
Notación: se define sen2α como (sen α)2. Lo mismo se aplica a las demás funciones trigonométricas.


Relaciones básicas
| Relación pitagórica |  |
|---|---|
| Identidad de la razón |  |
De estas dos identidades, se puede elaborar la siguiente tabla. Sin embargo, nótese que estas ecuaciones de conversión pueden devolver el signo incorrecto (+ ó −). Por ejemplo, si  la conversión propuesta en la tabla indica que
la conversión propuesta en la tabla indica que  , aunque es posible que
, aunque es posible que  . Para obtener el signo correcto se necesitará saber los valores para los cuales la función trigonométrica en cuestión es negativa o positiva.
. Para obtener el signo correcto se necesitará saber los valores para los cuales la función trigonométrica en cuestión es negativa o positiva.
 la conversión propuesta en la tabla indica que
la conversión propuesta en la tabla indica que  , aunque es posible que
, aunque es posible que  . Para obtener el signo correcto se necesitará saber los valores para los cuales la función trigonométrica en cuestión es negativa o positiva.
. Para obtener el signo correcto se necesitará saber los valores para los cuales la función trigonométrica en cuestión es negativa o positiva.| En términos de | 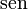 |  |  |  |  |  |
|---|---|---|---|---|---|---|
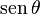 |  | 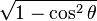 |  |  | 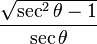 |  |
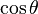 |  | 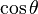 |  |  |  | 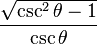 |
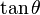 |  |  |  | 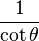 |  |  |
 |  |  |  | 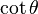 |  |  |
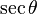 |  | 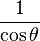 | 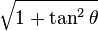 |  | 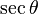 | 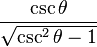 |
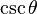 |  |  |  |  |  | 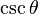 |
De las definiciones de las funciones trigonométricas:
Son más sencillas de probar en la circunferencia trigonométrica o goniométrica (que tiene radio igual a 1):
A veces es importante saber que cualquier combinación lineal de una serie de ondas senoidales que tienen el mismo período pero están desfasadas, es también una onda senoidal del mismo período pero con un desplazamiento de fase diferente. Dicho de otro modo:
Es llamada identidad trigonométrica fundamental, y efectuando sencillas operaciones permite encontrar unas 24 identidades más, muy útiles para problemas introductorios del tipo conocido el valor de la función seno, obtenga el valor de las restantes (sin tabla ni calculadora).
Por ejemplo, si se divide ambos miembros de "sen² + cos² = 1" por cos², se obtiene:
Ahora, dividiendo ambos miembros de la misma expresión por el sen², se obtiene:
Entonces puede expresarse la función seno según alguna otra conocida:
Ejemplo 2:
| [Expandir]
|
Teoremas de la suma y diferencia de ángulos
Pueden demostrarse según la Fórmula de Euler o mediante la proyección de ángulos consecutivos. La identidad de la tangente surge del cociente entre coseno y seno, y las restantes de la recíproca correspondiente.
[Expandir]   |
De lo que se sigue para determinados ángulos suplementarios:
Para ángulos opuestos:
Identidades del ángulo múltiple
Si Tn es el n-simo Polinomio de Chebyshev entonces
Identidades del ángulo doble, triple y medio
Pueden obtenerse remplazándolo y por x (o sea  ) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando
) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando  .
.
 ) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando
) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando  .
.| Fórmula del ángulo doble | |||
|---|---|---|---|
 |  |  |  |
| Fórmula del ángulo triple | |||
 | 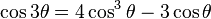 |  | |
| Fórmula del ángulo medio | |||
 | 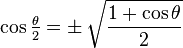 |  |  |
Producto infinito de Euler[editar]
Identidades para la reducción de exponentes
Resuelve las identidades tercera y cuarta del ángulo doble para cos²(x) y sen²(x).
| Seno |  |  |  | |
|---|---|---|---|---|
| Coseno | 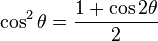 |  | 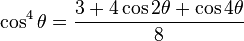 | 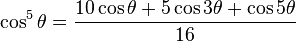 |
| Otros |  |  |
Paso de producto a suma
Puede probarse usando el teorema de la suma para desarrollar los segundos miembros.
[Expandir]    |
Paso de suma a producto
[Expandir]    |
Paso de diferencia de cuadrados a producto
- Deducción
1) recordando: que cateto opuesto sobre cateto adyacente
multiplicando
De tal manera que obtendremos:
aplicando esto en la ecuación inicial
multiplicando
De una manera análoga se halla el primer teorema.
Eliminar seno y coseno
A veces es necesario transformar funciones de seno y coseno para poderlas sumar libremente, en estos casos es posible eliminar senos y cosenos en tangentes.
Funciones trigonométricas inversas
Composición de funciones trigonométricas
|
|
|
| |
|
| |
|
| |
Fórmula de productos infinitos
| Seno | Coseno |
|---|---|
|
|
|
Fórmula de Euler
Teorema del Coseno
|
Teorema del seno
En todo triángulo se da la siguiente relación entre la longitud de sus lados a, b y c y el seno de sus respectivos ángulos opuestos A, B y C

Aplicación[editar]
El teorema del seno es usado con frecuencia para resolver problemas en los que se conoce un lado del triángulo y dos ángulos y se desea encontrar las medidas de los otros lados.
Definiciones exponenciales
La mayor parte de funciones trigonométricas admiten una formulación en términos de números complejos, algunos ejemplos:
| Función | Función inversa |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
























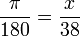

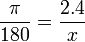

































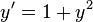



























































![\sen(n\;arcsen(x))= x\left[\sum_{k=0} (-1)^k \left(
\begin{matrix} n-1-k\\ k \end{matrix} \right)(2x)^{n-2k-1}\right]](https://upload.wikimedia.org/math/a/5/2/a528bd2712c51350961ed0531d80d8b8.png)







